Buscanos tambien en:

El Ovoide.

Es una curva plana cerrada compuesta por dos arcos de circunferencia iguales y otros dos desiguales. Tiene un eje de simetría. Puede decirse tambien que es medio ovalo en el que la otra mitad se ha sustituido por media circunferencia.

Su forma geométrica tiene gran importancia para el diseño del elemento mecanico llamado leva, utilizado en los motores de nuestros coches. La figura siguiente muestra una representación simple del funcionamiento de una leva.

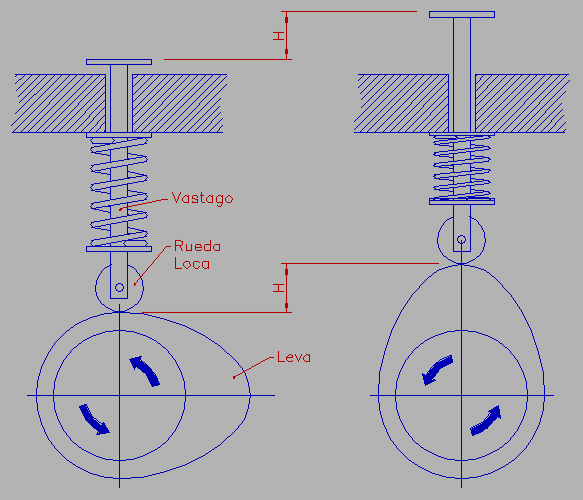
El funcionamiento de la leva consiste en convertir el movimiento circular excentrico, producido alrededor de un eje, en un movimiento alternativo vertical, y comunicarselo a un vastago en continuo contacto con ella, de modo que el vastago en su movimiento controla la apertura y cierre de las valvulas del motor en los momentos requeridos.

En la actualidad existen tecnicas especiales para el diseño de levas consistente en el desarrollo lineal del movimiento del vastago para, en función del mismo, obtener la forma del perfil de leva, que se asemeja al del ovoide, aunque en general no resulte identico.

Contruir un ovoide conocido su eje menor.

1.- Partimos del segmento AB como eje menor del ovoide. Trazamos su mediatriz, y con centro O, punto medio de AB la circunferencia de diámetro AB que corta la mediatriz anterior en un punto C.

2.- Se unen A y B con C, en estas dos rectas estarán los puntos de tangencia de los arcos.

3.- Con centro A y B se trazan dos arcos de radio AB hasta cortar a las rectas en los punto de tangencia D y E.

4.- Con centro C se traza el arco de radio CD que cierra el ovoide deseado.

Contruir un ovoide conocido su eje mayor.

1.- Partimos del segmento AB como eje mayor del ovoide, el cual se divide en seis partes iguales y se traza por la 2º división una perpendicular a AB que será el otro eje del ovoide.

2.- Con centro en la 2º división se traza una semicircunferencia que nos determina los puntos C y D.

3.- Con centro también en la 2º división se traza otra semicircunferencia que nos determina los puntos E y F, centros de los arcos del ovoide, los cuales se unen con la 5º división. En estas dos lineas rectas se encontraran los puntos de tangencia.

4.- Con centro en E se traza un arco de radio ED hasta la línea dibujada en el paso anterior obteniendose el punto de tangencia G, y se repite el proceso desde el punto F simétrico del E obteniendose el el otro punto de tangencia H.

5.- Con centro en la 5º división se traza la circunferencia que pasa por los puntos de tangencia obtenidos en el paso anterior y que cierra el ovoide.

Contruir un ovoide conocido sus dos ejes.

1.- Comenzaremos con en segmento AB, eje menor del ovoide, trazamos su mediatriz que nos determina el punto O. Con centro en O se traza una circunferencia que pase por A y por B, obteniendo los puntos C y E. Desde C trasladamos la medida del eje mayor CD, obteniendo los dos ejes AB y CD del ovoide.

2.- Con centro E y radio ED se traza una circunferencia. Con el mismo radio ED y centro A se traza otra circunferencia que determina el punto F.

3.- Se unen los puntos F y E y se traza la mediatriz del segmento obtenido que corta al eje menor en el punto G.

4.- Por simetría llevamos el punto G al otro lado del futuro ovoide obteniendo el punto H.

5.- Uniendo los puntos G y H con E y prolongando las lineas cortan a la circunferencia dibujada en el 2º paso en los dos puntos de tangencia del ovoide. Con los datos obtenido ya se puede dibujar el ovoide.

Cad-Projects espera que el articulo haya sido de utilidad. Si es así puedes imprimir una copia o recomendar a algún amigo usando los iconos de la barra superior. Volver arriba. No olvides visitar nuestro FORO si tienes dudas o preguntas sobre algun tema.

Artículos relacionados.

© Copyright 2011 Cad-Projects España. Todos los derechos reservados.