Fecha del artículo:
2011-08-08
La Elipse.
Propiedades:
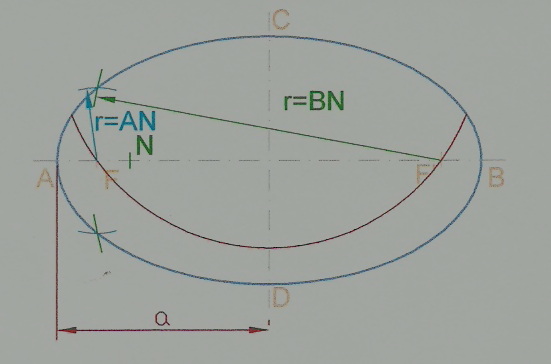
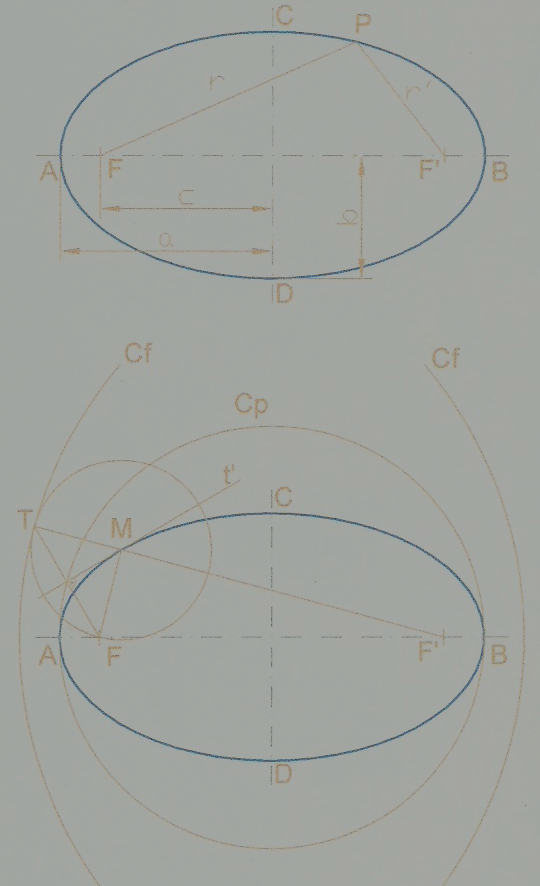
- Curva plana y cerrada cuyos puntos constituyen un lugar geométrico con la propiedad de que la suma de distancias de cada uno de sus puntos a otros dos fijos llamados focos es siempre constante e igual a 2a, longitud del eje mayor.
r + r’=2a. A r y r’ se les llama radios-vectores.
- El eje mayor AB se llama eje real, se representa por 2a.
- El eje menor CD se representa por 2b.
- Los focos están en el eje real, la distancia focal F-F’ se representa por 2c.
Entre a, b, y c existe la relación: a2=b2+c2
- La excentricidad e=c/a, mide el grado de achatamiento de la elipse.
e=0 → circunferencia e=1 → segmento
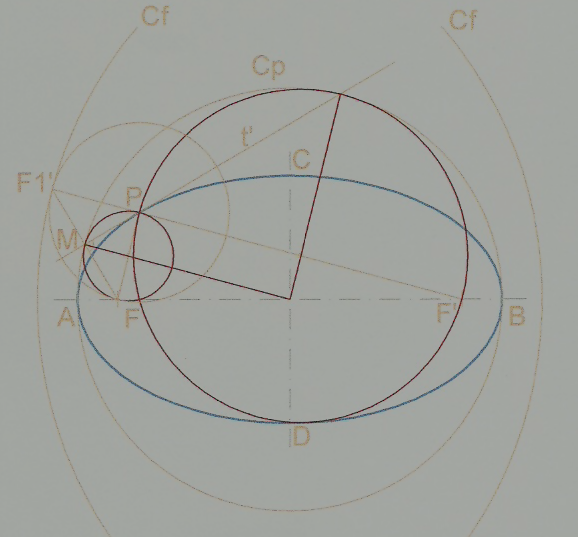
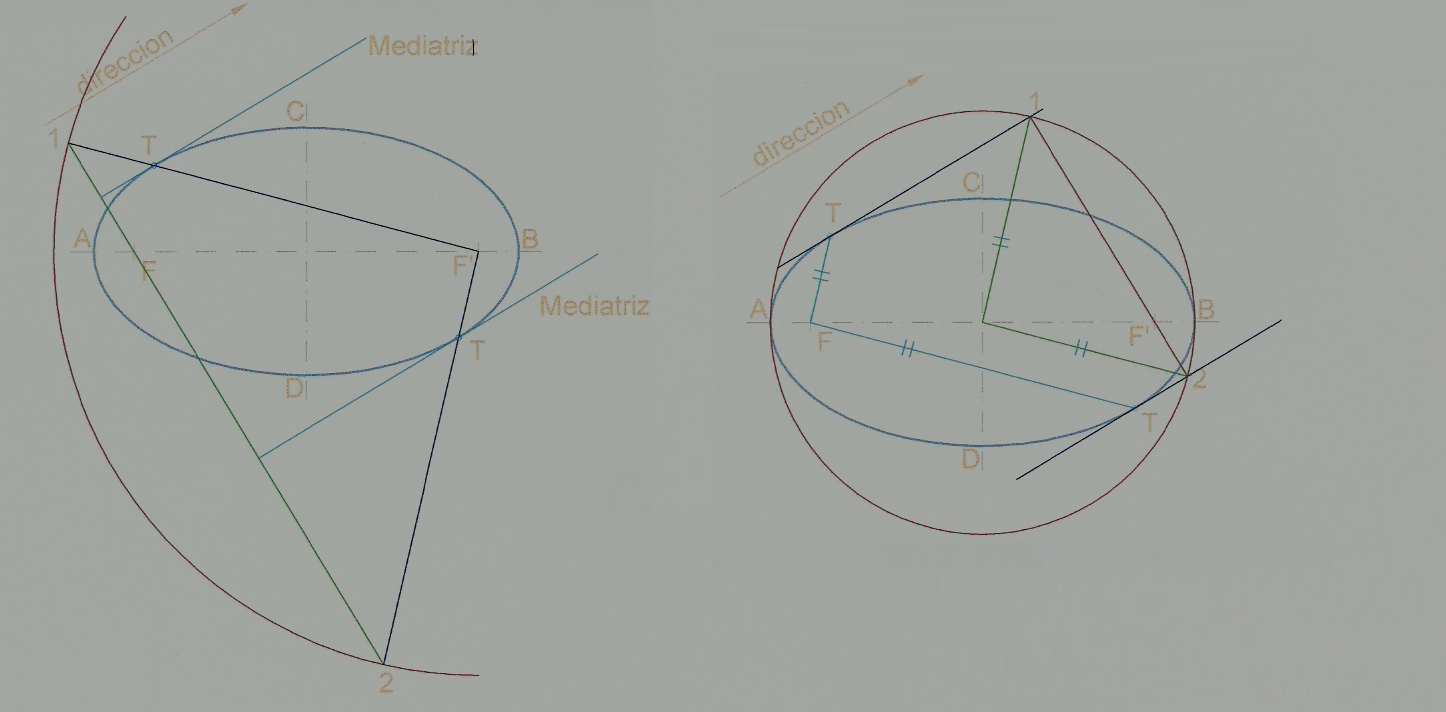
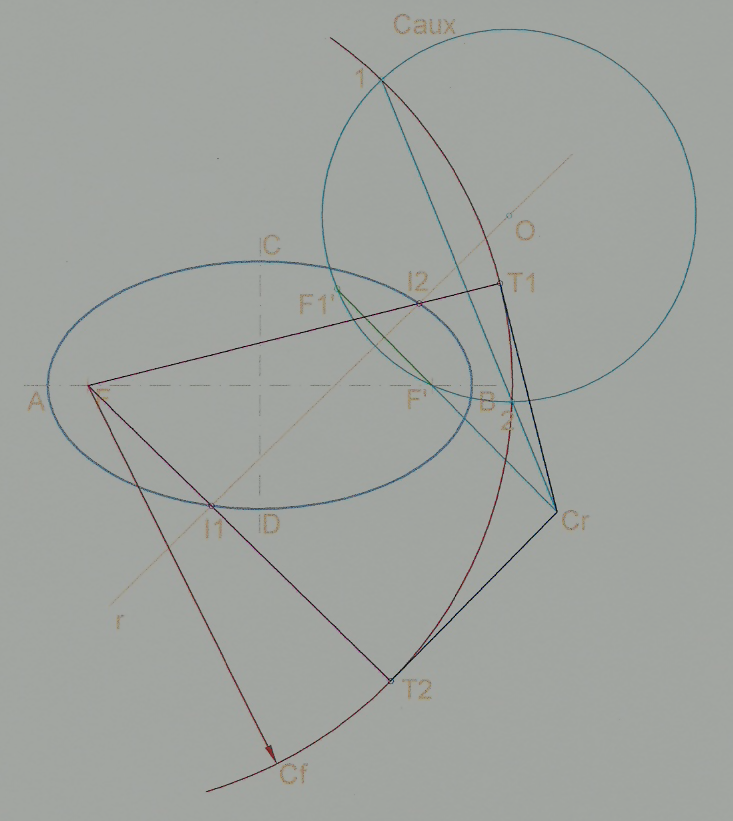
- La circunferencia principal tiene por centro el de la elipse y radio 2a, y es el lugar geométrico de los pies de las perpendiculares trazadas por los focos a cada una de las tangentes.
- Las circunferencias focales tienen por centro los focos y radio 2a. La elipse puede definirse como el lugar geométrico de los centros de las circunferencias que pasan por un foco y son tangentes a la circunferencia focal del otro foco.