Buscanos tambien en:

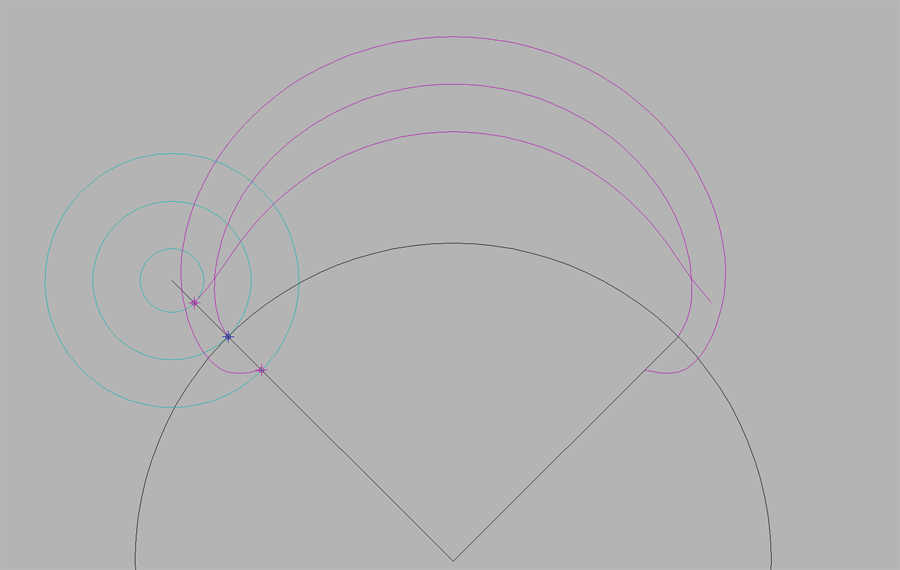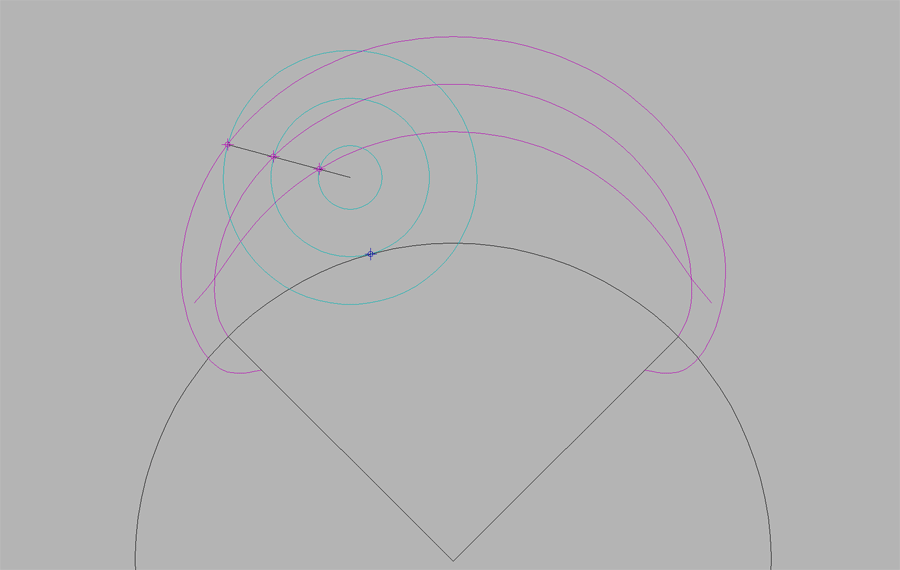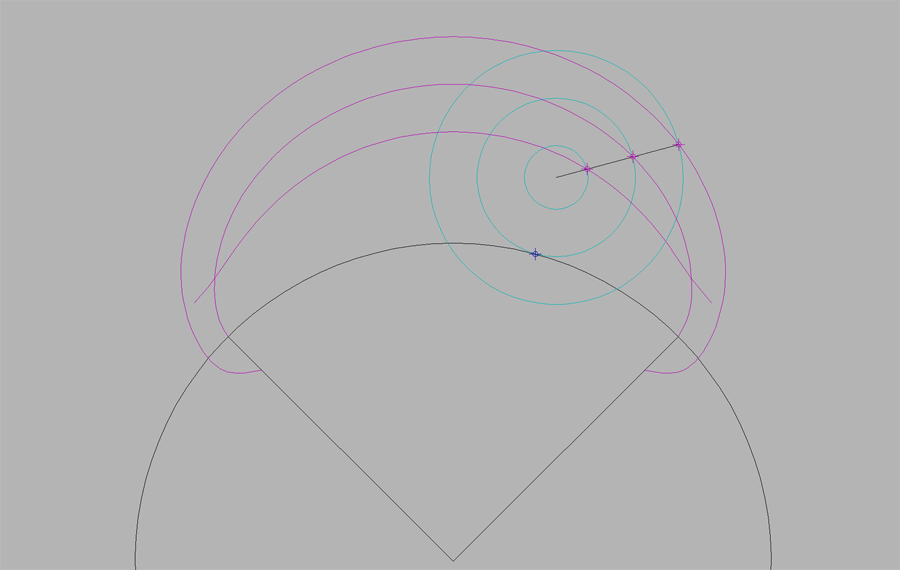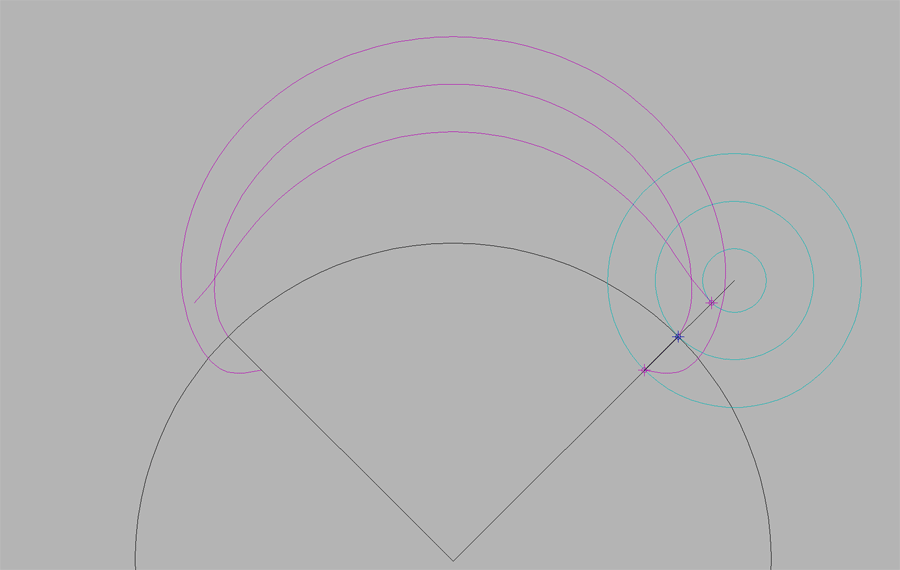
Epicicloide.

Se define como el lugar geométrico de las sucesivas posiciones de un punto P de una circunferencia generatriz o ruleta que rueda sin resbalar sobre otra circunferencia fija llamada base.

Pueden darse tres casos distintos, en función de las tres posibles posiciónes del punto P en la circunferencia:

- Si el punto P está en la ruleta, tendríamos una epicicloide normal.

- Si el punto P es exterior a la ruleta, tendríamos una epicicloide alargada.

- Si el punto P es interior a la ruleta tendríamos una epicicloide acortada.

Construcción de la epicicloide normal.

1.- El primer paso consiste en trazar un arco sobre la circunferencia base de longitud igual a circunferencia ruleta, para ello es necesario hallar el angulo central α que abarca el arco equivalente a la longitud de la ruleta

2 π R /2 π r = 360º /α

α = 360º r/R

α = 360 X 300/1200 = 90º

2.- Se divide la ruleta y el arco obtenido en un mismo número de partes, por ejemplo doce. Al hacer las divisiones en angulo central queda dividido tambien. En las prolongaciones de estas divisiones estaran los radios de la epicicloide.

3.- Con centro en O1 se trazan arcos que pasen por las divisiones obtenidas en la ruleta y por su centro. En las intersecciones del arco que pasa por el centro de la ruleta con las divisiones del angulo central se obtienen los puntos 1", 2", 3", ..., 12", centros de los radios de la epiciloide.

4.- Con centro en los puntos obtenidos anteriormente y radio r se van trazando arcos que cortan al arco que pasa por la división de la ruleta correspondiente obteniendose los puntos P1, P2, P3, ..., P12 de la epicicloide.

Construcción de la epicicloide alargada y acortada.

El metodo constructivo para estas variaciones es identico al de las cicloides correspondientes. A continuación ponemos unos ejemplos en el que se han obtenido los tres tipos de epicicloide. Para dibujarlas se ha utilizado Autocad^® y una macro de VBA^® que puede obtenerse en la seccíon de descargas.

Para dibujarlas se ha utilizado Autocad^® y una macro de VBA^®. Con esta sencilla macro se puede dibujar rapidamente cualquier tipo de curva ciclica. Hemos puesto esta macro en la sección de descargas, si estás registrado y conectado puedes descargar el programa pinchando el enlace siguiente: macro autocad curvas ciclicas.

Cad-Projects espera que el articulo haya sido de utilidad. Si es así puedes imprimir una copia o recomendar a algún amigo usando los iconos de la barra superior. Volver arriba. No olvides visitar nuestro FORO si tienes dudas o preguntas sobre algun tema.

Artículos relacionados.

© Copyright 2011 Cad-Projects España. Todos los derechos reservados.