Fecha del artículo:
2011-09-20
Haces ortogonales.
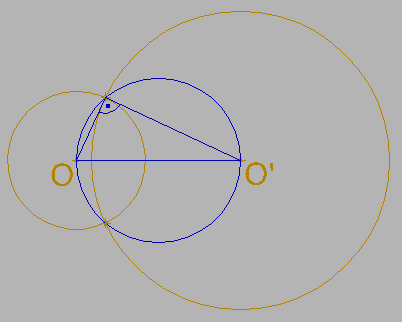
Se definen las circunferencias ortogonales como aquellas que se cortan de forma que las tangentes en los puntos de intersección forman noventa grados, pasando la tangente a cada curva por el centro de aquella a la que resulta ortogonal.
Cada haz de circunferencias corradicales lleva asociado otro haz de circunferencias ortogonales a las primeras. El eje radical de las definidoras del primer haz es la recta donde se sitúan los centros de las circunferencias del haz ortogonal. Del mismo modo, la recta que definen los centros de las circunferencias del primer haz es el eje radical de las del segundo haz.
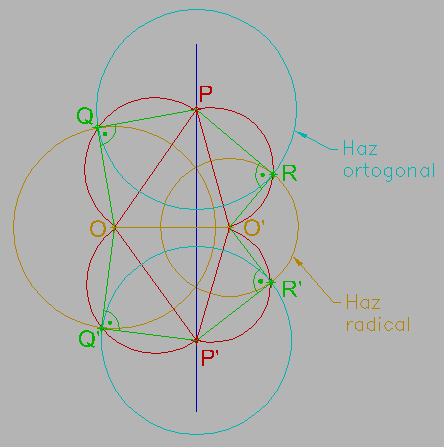
Para obtener un haz ortogonal a uno dado, partimos del haz radical definido por las dos circunferencias que se cortan; hallamos el eje radical de las mismas y tomamos un punto P cualquiera de dicho eje radical; trazamos desde P la tangente a una de las curvas del primer haz, siendo PQ o PR el valor del radio de una circunferencia ortogonal del segundo haz. Repitiendo el proceso, por ejemplo con P′, obtenemos cuantos elementos del haz ortogonal deseemos.




