Acceder

Nombre:

Clave:

 Registrarse

Buscanos tambien en:

Construcción avanzada de triangulos.

 

La resolución geométrica de triangulos es uno de los problemas más comunes que cualquier proyectista o diseñador suele encontrarse en su trabajo debido las múltiples aplicaciones prácticas que tienen dentro del ámbito técnico. La forma triangular es la unica estructura indeformable que existe, y cualquier polígono puede ser descompuesto en triangulos,  caracteristicas que los hacen muy util en replanteos o en el diseño de estructuras.

 

Son multiples los casos diferentes de resolución de triangulos que se nos pueden plantear, desde los más sencillos a casos en los que es necesario aplicar diferentes propiedades de los triangulos y de otras figuras geométricas.

 

A continuación veremos la construcción de algunos de ellos.

 

Consideraciones previas.

 

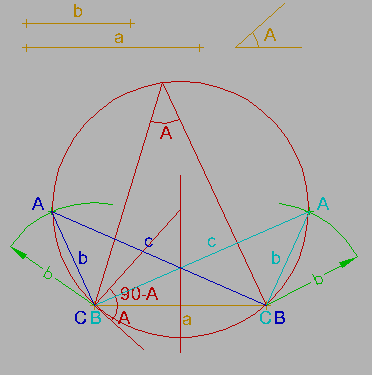
Para este capítulo seguiremos el criterio de definición de los datos mas común en triángulos, que consiste en nombrar mediante letras minúsculas los lados, y con la misma letra pero en mayúscula el vértice y el ángulo opuestos a cada lado.

 

Construir un triángulo conociendo un lado, su ángulo opuesto y otro lado.

 

 

 

 

1.- El primer paso sería construir el arco capaz del ángulo dado sobre su lado, ese arco será el lugar geométrico de los puntos que son el vértice opuesto al lado dado.

 

2.- Si desde un vértice cualquiera del lado dado se trazan arcos con radio el igual al otro lado dado cortaran al arco capaz en un punto que es vértice del triangulo buscado.

 

 

 

 

 

 

 

 

 

 

 

Construir un triángulo conociendo un lado, su ángulo opuesto y la altura.

 

 

 

 

 

El problema es parecido al anterior pero en este caso los vértices estarían en la intersección de la paralela al lado a la altura dada con el arco capaz, obteniéndose también las dos soluciones.

 

 

 

 

 

 

 

 

 

 

 

 

 

Construir un triángulo conociendo un lado, su altura correspondiente y otra altura.

 

 

 

 

1.- Desde uno de los vértices del lado dado se traza un arco de radio la altura del otro lado.

 

2.- Si desde el otro vértice se traza una tangente al arco anterior la línea será el lado correspondiente a esa altura.

 

3.- Trazando una paralela  al lado dado con la altura también dada se obtiene el vértice del triangulo.

 

 

 

 

 

 

Construir un triángulo conociendo las tres alturas.

 

 

 

 

 

1.- Se sitúan sobre tres rectas concurrentes en un punto O las medidas de las tres alturas.

 

2.- Se dibuja una circunferencia que pase por los tres puntos anteriores de manera parecida a la de la figura.

 

3.- Con esta figura vamos a relacionar el concepto de potencia de un punto respecto a una circunferencia que dice: Ha x ha = Hb x hb = Hc x hc = constante, con la definición del área del triángulo, que diría que el producto de cada lado de un triangulo por su altura es un valor constante, igual al doble del área.

 

4.- Por tanto, los segmentos obtenidos en el paso anterior representarían los lados de un triangulo semejante al buscado, pero con distintas alturas, por lo que construyendo dicho triangulo y situando sobre una de sus alturas el valor dado para esa altura se obtiene el tríangulo deseado.

 

 

 

 

 

 

 

Construir un triángulo conociendo las tres medianas.

 

 

 

Basándonos en que el punto de intersección de las tres medianas de un triangulo, el baricentro, dista 2/3 de cada vértice y 1/3 del punto medio de cada lado, y que en los paralelogramos el punto de corte de las dos diagonales esta en el punto medio de cada una de ellas se realiza la siguiente construcción.

 

1.- Se construye un triangulo abc de lados las dos terceras partes de cada mediana.

 

2.- Tomando un vértice cualquiera del triangulo hallamos su simétrico para construir un paralelogramo abcb’ o abcc’.

 

3.- A continuación se halla el simétrico de cualquiera de los otros dos vértices siempre sobre la prolongación de la diagonal del paralelogramo obteniéndose el punto c’ o a’ vértice del triangulo buscado.

 

4.- No importa cómo se posicionen los lados del triangulo o que vértices se utilice, el resultado será siempre el mismo triangulo simétrico a un lado u otro.

 

 

 

 

 

Construir un triángulo conociendo la altura, la mediana y la bisectriz de un mismo lado.

 

Basándonos en la propiedad que dice: en todo triangulo inscrito en una circunferencia se cumple que la bisectriz de un ángulo y la mediatriz del lado opuesto concurren en un punto de la circunferencia circunscrita al triangulo, se realiza la siguiente construcción:

 

1.- Se construye un triangulo rectángulo AHM con los datos de la altura y la mediana.

 

2.- Desde el punto M se traza una perpendicular que será mediatriz del triangulo buscado, y desde el punto A un arco de radio igual a la bisectriz que corta al triangulo anterior en el punto a. Uniendo A con a se obtiene el punto P intersección de la bisectriz con la mediatriz del triangulo buscado, por el que pasa la circunferencia circunscrita comentada en el enunciado.

 

3.- La circunferencia que buscamos pasara por A, por P y su centro estará en la mediatriz MP por tanto su centro O estará en la intersección de MP con la mediatriz de AP.

 

4.- Dibujando la circunferencia se obtienen los puntos B y C del triangulo buscado. El la figura se ve claramente que el triangulo cumple con la condiciones pedidas.

 

Cad-Projects espera que el articulo haya sido de utilidad. Si es así puedes imprimir una copia o recomendar a algún amigo usando los iconos de la barra superior. Volver arriba. No olvides visitar nuestro FORO si tienes dudas o preguntas sobre algun tema.

Artículos relacionados.

© Copyright 2011 Cad-Projects España. Todos los derechos reservados.