Buscanos tambien en:

Potencia de un punto respecto una circunferencia.

Sea la figura de la imagen en la que se parte de una circunferencia y un punto O exterior a la misma.

Trazamos dos secantes desde O, obteniendo cuatro puntos A, B, C y D. Pretendemos demostrar que el producto de la pareja de segmentos OA por OB es igual al obtenido con la otra pareja: OC por OD. Al resultado común de ambas operaciones se le llama potencia del punto O respecto a la circunferencia.

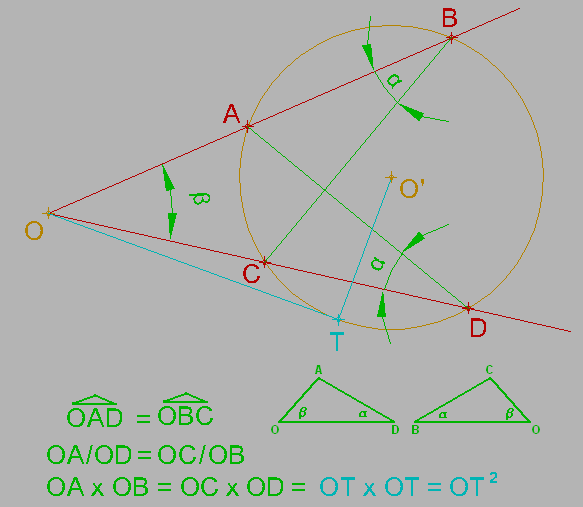
Demostración.

En la figura se producen dos triángulos semejantes el OAD y el OBC. La semejanza se sustancia que los ángulos en O son iguales, por estar limitados por los mismos lados. El ángulo en D del primer triángulo es igual al ángulo en B en el segundo, por estar ambos ángulos inscritos en la misma circunferencia y abarcar el mismo arco limitado por A y C.

Al tener dos ángulos iguales se infiere la igualdad del tercero, dado que la suma de los tres ángulos de un triángulo es siempre 180°.

Se cumple, por tanto, la igualdad entre las relaciones OA/OD y OC/OB. De la igualdad anterior se deduce que: OA · OB = OC · OD, como se quería demostrar, garantizando así la constancia de los productos de los segmentos obtenidos al trazar cualquier secante a una circunferencia desde un punto O exterior.

Si la recta es tangente a la circunferencia el valor de la potencia seguirá siendo el mismo, con lo que podemos expresar la igualdad OA x OB = OC x OD = OT².

Nota. Cuando el punto desde el que se quiere hallar la potencia pertenece al círculo interior de la circunferencia, la potencia adquiere un valor negativo pues los segmentos objeto de producto son de signo contrario.

Si el punto pertenece a la circunferencia la potencia es cero, y si el punto coincide con el centro de la circunferencia la potencia vale -r², siendo r el radio de la misma, siendo dicha potencia negativa por estar en el interior del circulo el punto desde el que se calcula.

Es fácil deducir por el teorema de pitagoras la propiedad de la potencia de un punto respecto una circunferencia que dice: que dicha potencia es igual a la diferencia entre el cuadrado de la distancia de O al centro y el cuadrado del radio de la circunferencia; OT²=OO′²-O′T².

Como ayuda orientadora para la demostración, proponemos trazar la secante que pase por el centro de la circunferencia, y aplicar la definición de potencia a los segmentos obtenidos. Se supone que la expresión a obtener ha de ser en función de la distancia de O al centro y del valor del radio.

El concepto de potencia se puede utilizar para hallar el segmento correspondiente a la media geométrica de dos segmentos dados OA y OB.

Se recuerda que la media geométrica de dos segmentos es la raíz cuadrada del producto de ambos; igualmente se acaba de definir la potencia de un punto respecto a una circunferencia como el producto de los segmentos obtenidos al trazar una secante desde el punto dado, o como el cuadrado del segmento de tangente definido por el punto dado y el de tangencia.

La conjunción de ambas definiciones nos ilumina sobre el proceso a seguir, consistente en llevar segmentos dados en una recta OAB. Trazamos una circunferencia cualquiera que contenga a los puntos  A y B, siendo el segmento de tangente OT la media geométrica pedida.

Cad-Projects espera que el articulo haya sido de utilidad. Si es así puedes imprimir una copia o recomendar a algún amigo usando los iconos de la barra superior. Volver arriba. No olvides visitar nuestro FORO si tienes dudas o preguntas sobre algun tema.

Artículos relacionados.

© Copyright 2011 Cad-Projects España. Todos los derechos reservados.