Buscanos tambien en:

Evolvente y Evolvente del circulo.

Evolvente.

Es el lugar geométrico de las sucesivas posiciones de un punto de una recta, tangente a una curva base o evoluta, cuando dicha tangente rueda sobre ella sin resbalar. Por tanto, la evoluta es el lugar geometrico de los centros de curvatura de una evolvente dada.

Podría también verse a la evolvente, en el caso particular de la evolente del circulo, como una inversa de la cicloide, en la que en lugar de ser la circunferencia la que rueda sobre una recta para ir describiendo sus puntos, es la recta la que gira sin deslizamiento sobre una circunferencia.

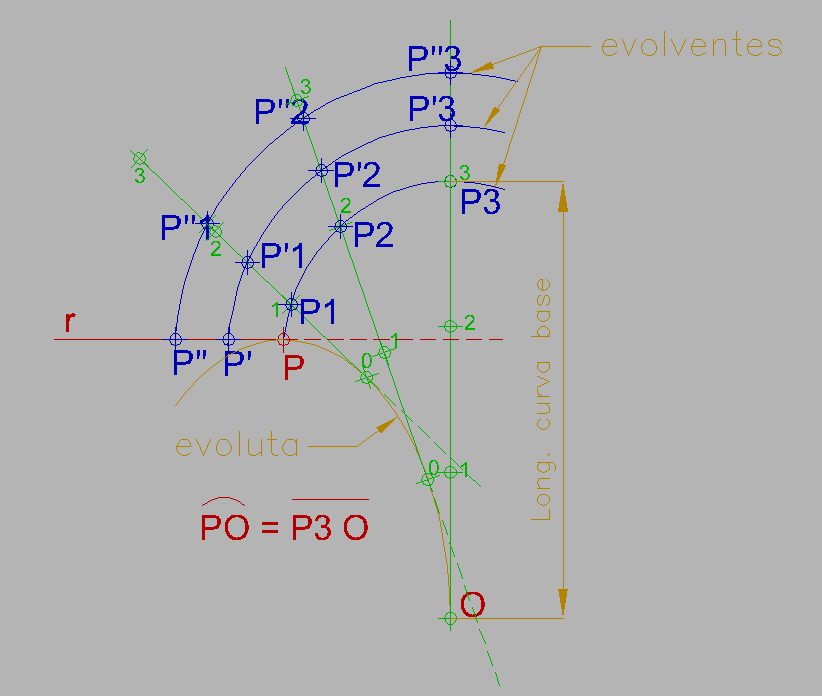
Para entender el concepto se puede imaginar una curva base o evoluta que tiene un cordel unido a un punto fijo O que podemos enrollar y desenrollar. Si lo tomamos por un punto P y vamos desenrrollando manteniendolo tenso, la curva descrita por el punto sería una evolvente. Tomando otros puntos del hilo se obtienen nuevas evolventes, de modo que a cada evoluta le corresponden infinitas evolventes.

Evolvente del circulo.

Cuando la curva base es una circunferencia se está ante un caso particular de este tipo de curvas. En la figura puede observarse la circunferencia de base, de radio r, y la tangente a la misma t, cuyo punto R genera la evolvente. Por definición el arco PQ es igual a la longitud del segmento RQ.

Cualquier tangente a la evolvente es siempre perpendicular a una recta tangente a la circunferencia base.

Los perfiles de los dientes de las ruedas dentadas suelen trazarse según arcos de evolvente de circulo.

Construcción de la evolvente del circulo.

1.- El primer paso sería dividor la circunferencia en un nº de partes iguales, por ejemplo doce ver división de una circunferencia en un numero de partes iguales.

2.- Se obtiene la rectificación de la circunferencia y se divide el segmento en el mismo número de partes iguales que la circunferencia, ver división de un segmento en un número de partes iguales.

3.- Se trazan tangentes a la circunferencia por los puntos obtenidos de su division y sobre esas tangentes se tomara tantan veces como corresponda la medida obtenida de dividir el segmento rectificacion de la circunferencia.

4.- Repitiendo el procedimiento se obtienen los puntos P1, P2, P3, ..., P12 de la evolvente del circulo dado,

Cad-Projects espera que el articulo haya sido de utilidad. Si es así puedes imprimir una copia o recomendar a algún amigo usando los iconos de la barra superior. Volver arriba. No olvides visitar nuestro FORO si tienes dudas o preguntas sobre algun tema.

Artículos relacionados.

© Copyright 2011 Cad-Projects España. Todos los derechos reservados.