Conectate para poder poner tu imagen de perfil. |
Aún no estas conectado.Utiliza tu nombre y clave para hacerlo. Si todavía no tienes una Pincha aquí para iniciar el registro. |

Conectate para poder poner tu imagen de perfil. |
Aún no estas conectado.Utiliza tu nombre y clave para hacerlo. Si todavía no tienes una Pincha aquí para iniciar el registro. |



  Cad-Projects espera que el articulo haya sido de utilidad.Si es así puedes imprimir una copia o recomendar a algún amigo usando los iconos de la barra superior. Volver arriba. No olvides visitar nuestro FORO si tienes dudas o preguntas sobre algun tema. |

Usuario |
Asunto |
Fecha |
|---|---|---|
Eduardo Antonio Prez |
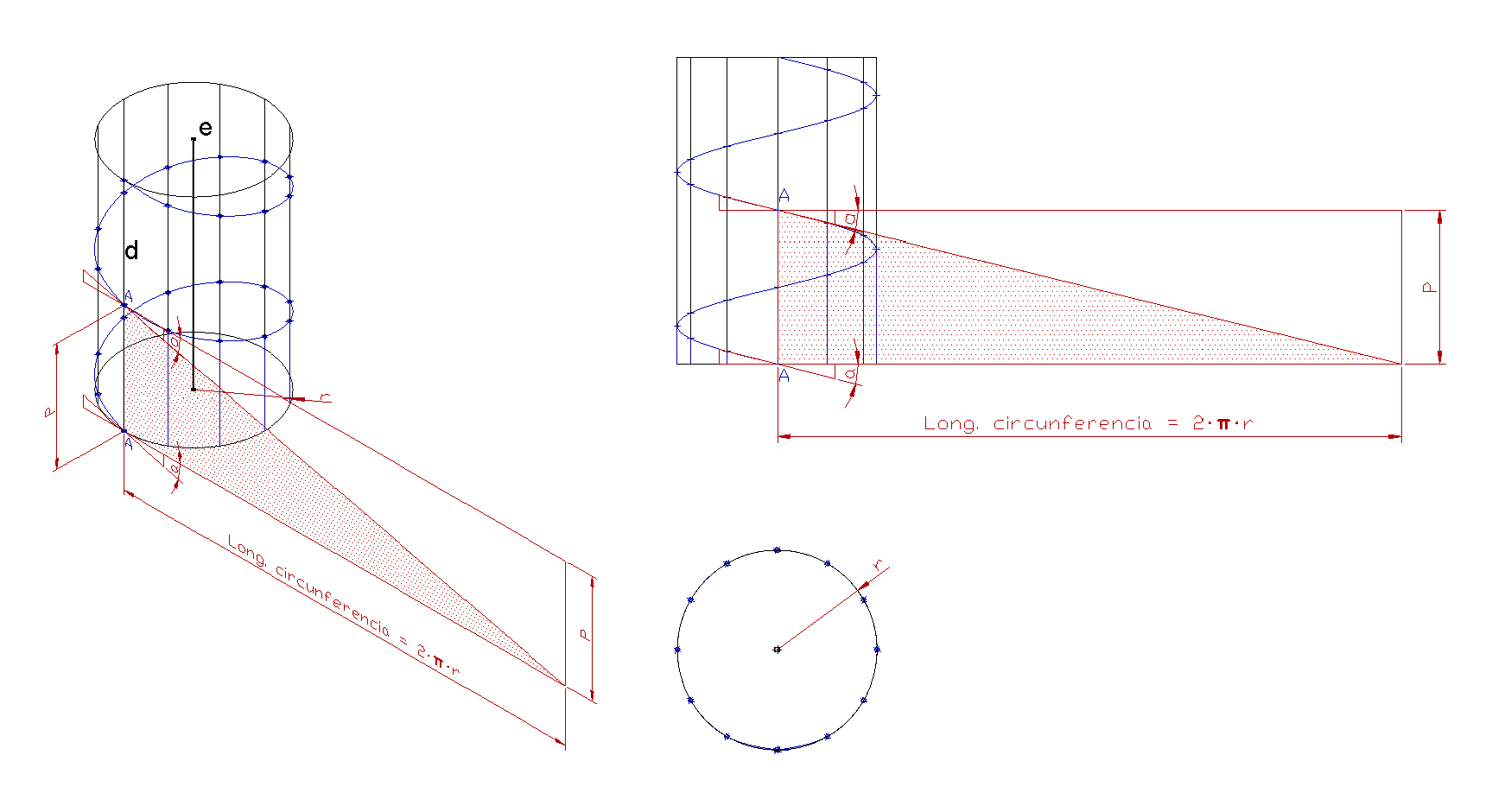
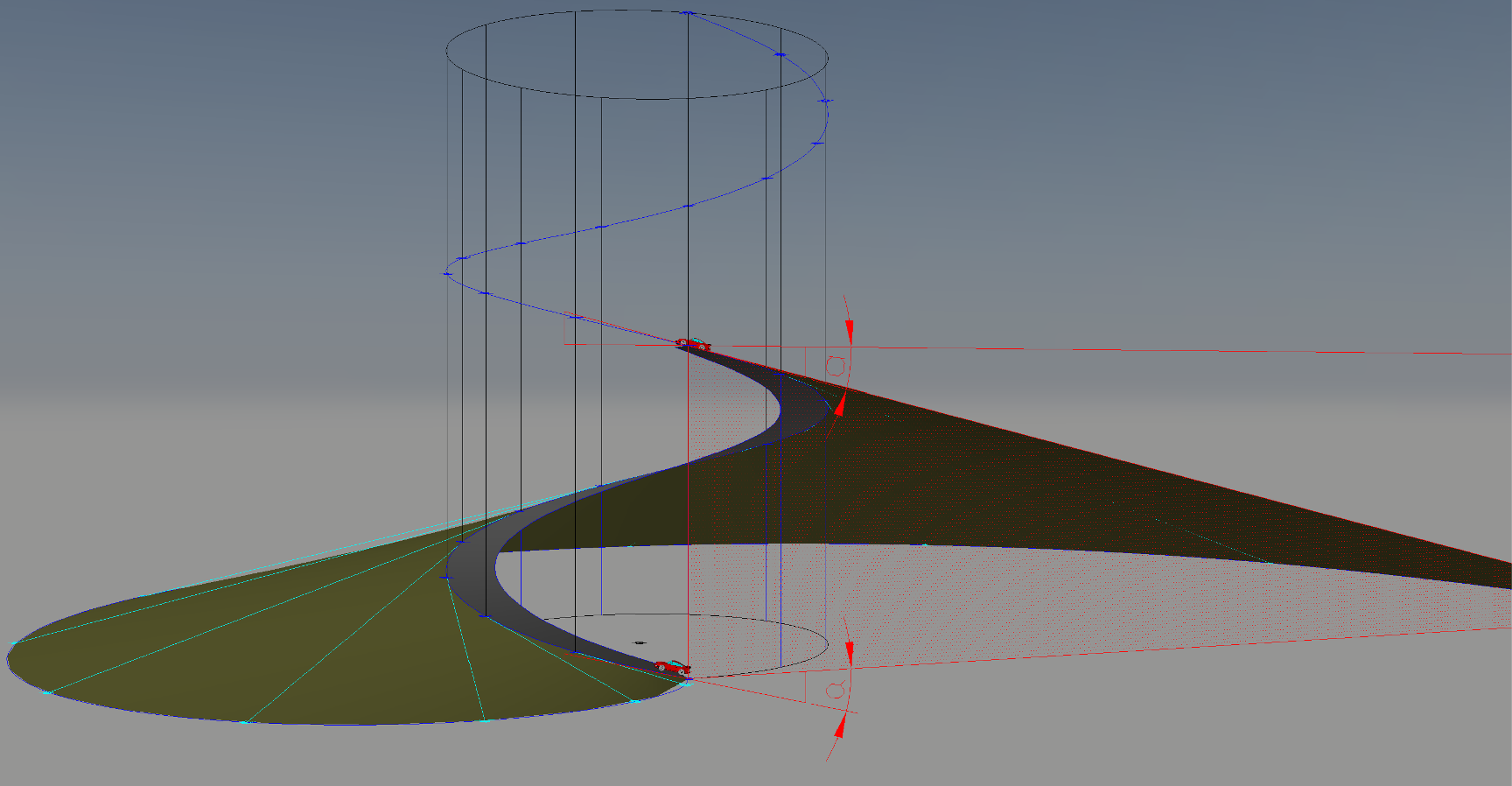
Desarrollo en el plano de una helicoide tipo transportadora de tornillo sin fin |
2015-05-10 10:17:17 |
Mensaje |
|---|
Estimados:No consigo desarrollar en el plano, para poder construirla, un espira de paso 300 mm, diámetro exterior 300 mm, diámetro interior (eje) 32 mm. Pueden Uds. ayudarme? Saludos cordiales Eduardo Prez |