Artículos publicados o editados recientemente.
Dentro de todas las categorías.
Artículo Nº46.
Fecha
2011-09-20
|
El eje radical de dos circunferencias es el lugar geométrico de los puntos que tienen igual potencia respecto a ambas. Tiene gran utilidad para la obtención de puntos de tangencia de un enlace.
El eje radical de dos circunferencias es el lugar geométrico de los puntos que tienen igual potencia respecto a ambas.

Se demuestra que este lugar geométrico es una recta perpendicular a la definida por los centros de ambas circunferencias, por lo que sería suficiente con obtener un punto de dicha recta para su definición. Por tanto, si trazamos la tangente común a dos circunferencias, y hallamos el centro del segmento definido por los puntos de tangencia, podemos afirmar que dicho punto pertenece al eje radical buscado, pues el cuadrado de su distancia a cada punto de tangencia es el valor de la potencia de ese punto respecto a las circunferencias dadas. La perpendicular a la recta OO’ trazada desde el punto medio antes hallado constituye el eje radical buscado.
Si las circunferencias se cortan, el eje radical queda definido por los puntos de corte.
Si son tangentes el eje radical es la tangente común.
Si una circunferencia es interior, a la otra, requiere una construcción especial que procedemos a justificar a continuación.
|
Artículo Nº47.
Fecha
2011-09-20
|
Se define potencia de un punto respecto una circunferencia al resultado que relaciona las longitudes de segmentos de rectas que pasan por dicho punto y cortan a la circunferencia.
Sea la figura de la imagen en la que se parte de una circunferencia y un punto O exterior a la misma.
Trazamos dos secantes desde O, obteniendo cuatro puntos A, B, C y D. Pretendemos demostrar que el producto de la pareja de segmentos OA por OB es igual al obtenido con la otra pareja: OC por OD. Al resultado común de ambas operaciones se le llama potencia del punto O respecto a la circunferencia.
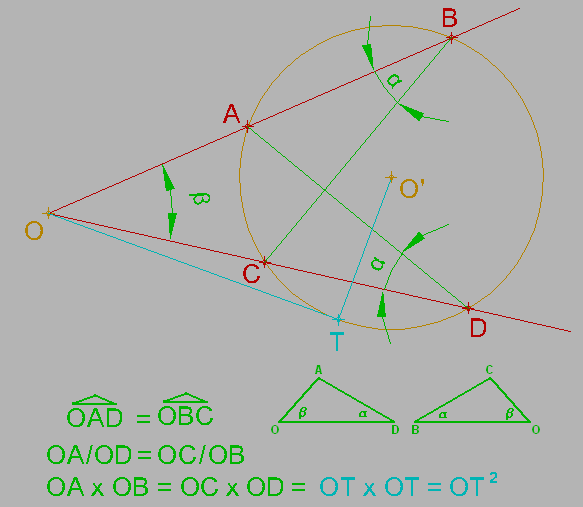
Demostración.
En la figura se producen dos triángulos semejantes el OAD y el OBC. La semejanza se sustancia que los ángulos en O son iguales, por estar limitados por los mismos lados. El ángulo en D del primer triángulo es igual al ángulo en B en el segundo, por estar ambos ángulos inscritos en la misma circunferencia y abarcar el mismo arco limitado por A y C.
Al tener dos ángulos iguales se infiere la igualdad del tercero, dado que la suma de los tres ángulos de un triángulo es siempre 180°.
Se cumple, por tanto, la igualdad entre las relaciones OA/OD y OC/OB. De la igualdad anterior se deduce que: OA · OB = OC · OD, como se quería demostrar, garantizando así la constancia de los productos de los segmentos obtenidos al trazar cualquier secante a una circunferencia desde un punto O exterior.
Si la recta es tangente a la circunferencia el valor de la potencia seguirá siendo el mismo, con lo que podemos expresar la igualdad OA x OB = OC x OD = OT2.
|
Artículo Nº48.
Fecha
2011-09-20
|
SimetrÃa
Click para ver más
Se dice que dos figuras son simétricas, respecto a un punto o a una recta, cuando haciendo girar mentalmente una de ellas alrededor de este punto o recta, coinciden exactamente la una sobre la otra.
La simetrÃa también puede aplicarse como transformación geométrica y se vera también en su capitulo correspondiente.
Se dice que dos figuras son simétricas, respecto a un punto o a una recta, cuando haciendo girar mentalmente una de ellas alrededor de este punto o recta, coinciden exactamente la una sobre la otra.
La simetría también puede aplicarse como transformación geométrica, y se puede ver, de manera más amplia, en en articulo relativo a simetría plana.

Simetria central respecto a un punto.
Se dice que dos puntos AA′ son simetricos respecto a un tercero O, cuando estan sobre una misma recta y equidistan del punto central O.
Simetria axial respecto a un eje.
Se dice que dos puntos AA′ son simetricos respecto a un eje O, cuando estan sobre una recta perpendicular al eje y equidistan de el.
Simetria con respecto a un plano.
Una figura sólida es simétrica con respecto a un plano que la corta, si todos los elementos geométricos de una parte, puntos, segmentos, poligonos, etc., tienen su respectiva simetría en la otra .
La figura de ejemplo es simetrica respecto al plano YZ, pero asimetrica respecto al otro plano XZ.
|
Artículo Nº49.
Fecha
2011-09-20
|
Escalas
Click para ver más
Escala es la relación que existe entre la representación gráfica de un objeto (dibujo) y el objeto en la realidad. Las escalas pueden ser de ampliación o de reducción y para unificar criterios están normalizadas según UNE 1 026-75 y DIN 823.
Hay casos, en los que por tratarse de objetos excesivamente grandes o demasiado pequeños, es conveniente reducir o ampliar el dibujo de los mismos, con una proporción adecuada. De lo contrario, sería necesario dibujar sobre papeles de dimensiones exageradas o conformarse con la imposibilidad de concretar detalles imprescindibles.
Escala es la relación que existe entre la representación gráfica del objeto (dibujo) y el objeto en la realidad.
Con la figura de la derecha se quiere poner de manifiesto la relación existente entre la representación gráfica del objeto y el objeto real.
Aplicación de escalas.
Determinación de la escala a que está realizado un dibujo:
Escala = Dibujo / Realidad
Determinación de las dimensiones reales de una figura dibujada a escala:
Realidad = Dibujo / Escala
Determinación de las dimensiones de los segmentos que componen el dibujo:
Dibujo = Escala x Realidad
|
Artículo Nº50.
Fecha
2011-09-20
|
Proporcionalidad es la relación que guardan dos figuras semejantes. Su valor se obtiene de los cocientes entre lados homólogos, siendo este siempre un valor constante.
Sean los dos números a y b, se dice que otra pareja de números c y d es proporcional a la primera cuando se cumple que los resultados de los cocientes realizados entre los elementos de cada pareja adquieren el mismo valor.
Así: a / b = c / d
Teorema de Thales.
Dadas dos rectas concurrentes que resultan cortadas por una serie de transversales paralelas entre sí, se cumple la proporcionalidad entre los segmentos que el segundo sistema de rectas paralelas produce en el primer sistema de concurrentes.
Concepto de cuarta proporcional. Construcción gráfica.

Sean los segmentos a, b y c de la figura, un segmento x es cuarta proporcional de los tres anteriores cuando se cumple la relación: a / b = c / x
Una forma de obtener la magnitud x sería mediante operaciones numéricas midiendo los segmentos. A nivel geométrico se resuelve aplicando el Teorema de Thales antes expuesto, situando los segmentos dados sobre dos rectas que formen un ángulo cualquiera, y a partir de su vértice común, de forma que en una se sitúan los segmentos de una fracción y en la otra el segmento de la otra fracción. Uniendo el extremo a con el de c y trazando una paralela por el otro extremo de b se obtiene E que define el segmento x correspondiente a la cuarta proporcional.
|
Más artículos
Cad-Projects espera que los artículos sean de utilidad.
Si es así puedes imprimir una copia o recomendar a algún amigo usando los iconos de la barra superior. Visita nuestro FORO. Si tienes dudas o preguntas sobre algun tema allí podras resolverlas.





