Artículos publicados o editados recientemente.
Dentro de todas las categorías.
Artículo Nº66.
Fecha
2011-09-20
|
El Ovalo
Click para ver más
Es una curva plana cerrada compuesta de cuatro arcos de circunferencia iguales dos a dos. Tiene dos ejes de simetria perpendiculares entre sÃ.
Es una curva cerrada y plana compuesta de cuatro arcos de circunferencia iguales dos a dos. Tiene dos ejes de simetria perpendiculares entre sí.
Es interes del estudio de este tipo de curvas radica en que es la construccion admitida dentro del Dibujo Industrial como aproximación al trazado de circunferencias en Perspectiva Isometrica, que como se sabe, en proyección isometrica, al igual que en cualquie otro tipo de proyección, las circunferencias proyectadas en planos oblicuos se convierten en elipses, que por su trazado a base de puntos resulta algo engorrosa.
En la figura puede verse la aplicacion del ovalo para el trazado de los circulos inscritos en las caras de un cubo tangentes a sus cuatro lados. Como se aprecia en perspectiva isometrica las caras cuadradas del cubo se convierten en rombos y el circulo se convierte facilmente en el ovalo inscrito en un rombo.
Las plantillas de ovalos son muy utiles para el trazado de circunferencias y arcos en isometrica, sobre todo en labores de croquizado.
|
Artículo Nº67.
Fecha
2011-09-20
|
Se define como el lugar geométrico de los puntos con la propiedad de que la diferencia de distancias de cada uno de ellos a otros dos puntos fijos llamados focos es siempre constante.
Propiedades:
- Curva plana, abierta de dos ramas cuyos puntos constituyen un lugar geométrico con la propiedad de que la diferencia de distancias a otros dos fijos llamados focos es siempre constante e igual a 2a=AB, longitud del eje real r-r’=2a.

- El eje mayor AB se llama eje real, se representa por 2a.
- El eje menor CD se representa por 2b y se llama eje imaginario porque no tiene puntos comunes con la curva.
- Los focos están en el eje real, la distancia focal F-F’ se representa por 2c.
- Entre a, b, y c existe la relacion: a2=b2+c2
- La excentricidad e=c/a 1
- La circunferencia principal tiene por centro O y radio a, y es el lugar geométrico de los pies de las perpendiculares trazadas por los focos a cada una de las tangentes.
- Las circunferencias focales tienen por centro los focos y radio 2a. La hipérbola, como la elipse, puede definirse como el lugar geométrico de los centros de las circunferencias que pasan por un foco y son tangentes a la circunferencia focal del otro foco.
|
Artículo Nº68.
Fecha
2011-09-20
|
Se define como el lugar geométrico de los puntos que equidistan de uno fijo F, llamado foco, y de una recta fija d, llamada directriz.

Propiedades:
- Curva plana abierta y de una rama. Se define como el lugar geométrico de los puntos que equidistan de uno fijo F, llamado foco, y de una recta fija d, llamada directriz. Tiene un vértice y V un eje de simetría que pasa por V y por el foco y es perpendicular a la directriz. La tangente en el vértice de la curva es paralela a la directriz.
- Se llama 2p a la longitud de la cuerda que es perpendicular al eje en el foco, p es el parámetro que define la parábola. El vértice como cualquier otro punto equidista de la directriz y el foco p/2.
- Los radios vectores del punto O son QN y QE.
- La directriz d hace de circunferencia focal de la parábola, en este caso de radio infinito. Según esto la directriz es el lugar geométrico de los puntos simétricos del foco respecto de cada tangente. F’ es el simétrico de E respecto la tangente t.
- La tangente en el vértice hace de circunferencia principal, según esto es el lugar geométrico de los pies de las perpendiculares trazadas por los focos a cada una de las tangentes.
|
Artículo Nº69.
Fecha
2011-09-20
|
La Elipse
Click para ver más
Se define como el lugar geométrico de los puntos con la propiedad de que la suma de distancias de cada uno de ellos a otros dos puntos fijos llamados focos es siempre constante.
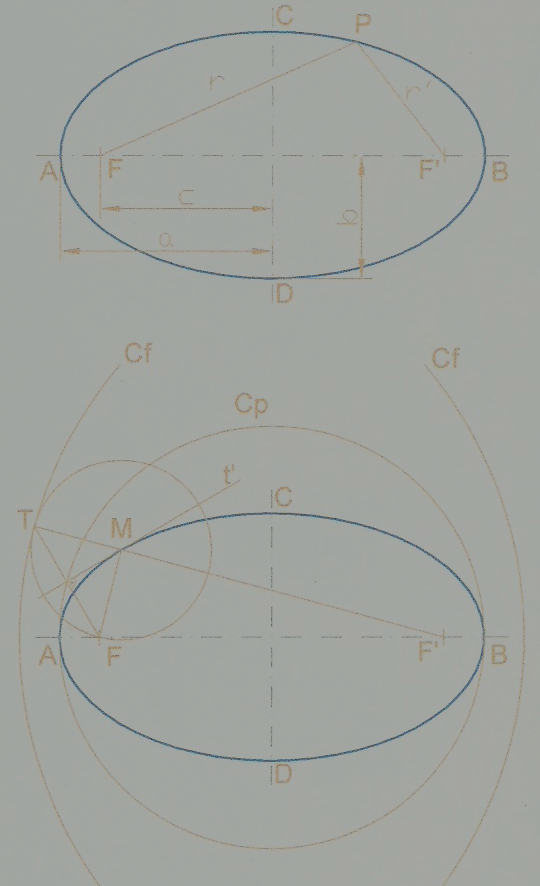
pan> de cada uno de sus puntos a otros dos fijos llamados focos es siempre constante e igual a 2a, longitud del eje mayor.
r + r’=2a. A r y r’ se les llama radios-vectores.
- El eje mayor AB se llama eje real, se representa por 2a.
- El eje menor CD se representa por 2b.
- Los focos están en el eje real, la distancia focal F-F’ se representa por 2c.
Entre a, b, y c existe la relación: a2=b2+c2
- La excentricidad e=c/a, mide el grado de achatamiento de la elipse.
e=0 → circunferencia e=1 → segmento
- La circunferencia principal tiene por centro el de la elipse y radio 2a, y es el lugar geométrico de los pies de las perpendiculares trazadas por los focos a cada una de las tangentes.
- Las circunferencias focales tienen por centro los focos y radio 2a. La elipse puede definirse como el lugar geométrico de los centros de las circunferencias que pasan por un foco y son tangentes a la circunferencia focal del otro foco.
|
Artículo Nº70.
Fecha
2011-09-20
|
Enlaces.
Click para ver más
Se llama enlace a la unión armonica de dos o más lÃneas, ya sean curvas o rectas, de modo que parezcan una sola lÃnea continua. Los enlaces se realizan mediante arcos y rectas tangentes. Una recta tangente es la que toca a la curva en un único punto, resultando perpendicular al radio que une dicho punto con el centro de la curva.
Se llama enlace a la unión armonica de dos o más líneas, ya sean curvas o rectas, de modo que parezcan una sola línea continua. Los enlaces se realizan mediante arcos y rectas tangentes. Una recta tangente es la que toca a la curva en un único punto, resultando perpendicular al radio que une dicho punto con el centro de la curva.
Para efectuar un enlace de forma correcta hay que realizar una serie de trazados que se indican a continuación:

-
Se determina el centro del arco o circunferencia, por medio de trazados geometricos apropiados.
-
Se determinan los puntos de tangencia, con objeto de saber donde ha de comenzar el enlace y dónde ha de terminar.
-
Se traza el arco de enlace.
|
Más artículos
Cad-Projects espera que los artículos sean de utilidad.
Si es así puedes imprimir una copia o recomendar a algún amigo usando los iconos de la barra superior. Visita nuestro FORO. Si tienes dudas o preguntas sobre algun tema allí podras resolverlas.





