Artículos publicados o editados recientemente.
Dentro de todas las categorías.
Artículo Nº51.
Fecha
2011-09-20
|
Semejanza
Click para ver más
Se dice que dos figuras son semejantes cuando teniendo la misma forma varÃan de tamaño, de modo que las medidas de los segmentos homólogos son proporcionales y cumpliéndose además la igualdad de los ángulos correspondientes.
La semejanza puede aplicarse también como transformación geométrica para conseguir figuras proporcionales a una dada, muy útil para poder obtener las distintas escalas.
Iniciamos el estudio de la Semejanza Geométrica, dando una serie de definiciones y propiedades básicas que necesitamos para el desarrollo teórico de los artículos tratados a continuación a este. No obstante volveremos sobre este concepto en el capítulo de transformaciones geométricas, ya que, como se verá, la semejanza se puede descomponer como producto de dos transformaciones, en concreto de una homotecia por un giro, por tanto, lo que a continuación se expone será ampliado en el correspondiente capitulo.
Conceptos. Definiciones y propiedades basicas de semejanza.
Decimos que dos figuras son semejantes cuando tienen la misma forma aunque distinto tamaño, independientemente de la posición relativa de ambas. Lo anterior se traduce en una igualdad entre los ángulos correspondientes de las dos figuras.
La figura representa dos casos de figuras semejantes, uno con los lados correspondientes paralelos y otro sin cumplir esta condición. En ambos ejemplos podemos decir que las figuras son semejantes, al cumplirse todos los términos de la definición presentada. En la primera, diremos que es una semejanza directa, y en la segunda inversa, en funcion del sentido en que se nombran los vértices correspondientes
En el supuesto de no disponer de un elemento de verificación de medidas angulares para apreciar la semejanza entre dos figuras dadas en posibles casos dudosos, podemos realizar una construcción indicada en la figura, consistente en llevar sobre dos rectas concurrentes las medidas de los lados hipotéticamente homólogos. La proporcionalidad entre los lados de las dos formas se cumplirá cuando las rectas definidas por las parejas de puntos correspondientes resulten paralelas entre sí en la construcción que estamos describiendo. Esta proporcionalidad implica la semejanza de las figuras y, por tanto, la igualdad entre los ángulos correspondientes.
|
Artículo Nº52.
Fecha
2011-09-20
|
Se dice que dos figuras o dos sólidos son equivalentes, cuando tienen igual área o volumen, expresada mediante un mismo valor numérico y en las mismas unidades de medida, aun teniendo forma distinta.
Se dice que dos figuras o dos sólidos son equivalentes, cuando tienen igual área o volumen, expresada mediante un mismo valor numérico y en las mismas unidades de medida, aun teniendo forma distinta.
La equivalencia trata de obtener figuras en las que la forma sea distinta pero con igual área, por lo que la dimension o tamaño de la figura mas o menos se mantiene. Durante nuestra historia fue muy conocido el problema de la cuadratura del circulo que junto a la triseccion del angulo y la duplicación del cubo, fue uno de los problemas clásicos de la Geometría en la antigua Grecia. Se ha demostrado que estos tres problemas, en general, son imposibles de resolver usando únicamente regla y compás, aunque son muy recurridas las aproximaciones.
Triangulo equivalente a uno dado manteniendo un lado.

Dado el triángulo ABC:
1.- Trazamos una recta r, paralela al lado que se desea mantener y que pase por su vértice opuesto. Todos los puntos de esa paralela tienen la misma altura H con respecto a ese lado.
2.- Si tomamos un punto C′ sobre la recta paralela r y lo unimos con A y B, el triángulo resultante es equivalente al triángulo ABC dado.
3.- Si tomamos un punto C" sobre la recta paralela r y lo unimos con A y B, el triángulo resultante es equivalente al triángulo ABC dado.
Aplicando esta construcción se puede reducir el numero de lados de un polígono cualquiera. Ejemplo 5.
|
Artículo Nº53.
Fecha
2011-09-20
|
Igualdad
Click para ver más
Se dice que dos figuras planas son iguales cuando sus lados y ángulos están dispuestos de modo que superponiendo una sobre otra coinciden exactamente confundiéndose en una sola.
Se dice que dos figuras planas son iguales cuando sus lados y ángulos están dispuestos de modo que superponiendo una sobre otra coinciden exactamente confundiéndose en una sola.
A continuación se verán los distintos metodos para obtener una figura igual a una dada.
Por triangulación.
Dada la figura ABCDE que se quiere reproducir observamos que puede descomponerse en tres triángulos ABC , ABD y ABE :
1.- Se traza un nuevo segmento A’B’ igual al AB y sobre el se construye el triángulo igual al A’B’E’, igual al ABE.
2.- Sobre el mismo segmento A’B’ se construye un segundo triángulo A’B’C’, igual al ABC.
3.- Sobre el mismo segmento A’B’ se construye un tercer triángulo A’B’D’, igual al ABD.
4.- Uniendo los puntos obtenidos se obtiene una figura igual a la dada.
|
Artículo Nº54.
Fecha
2011-09-20
|
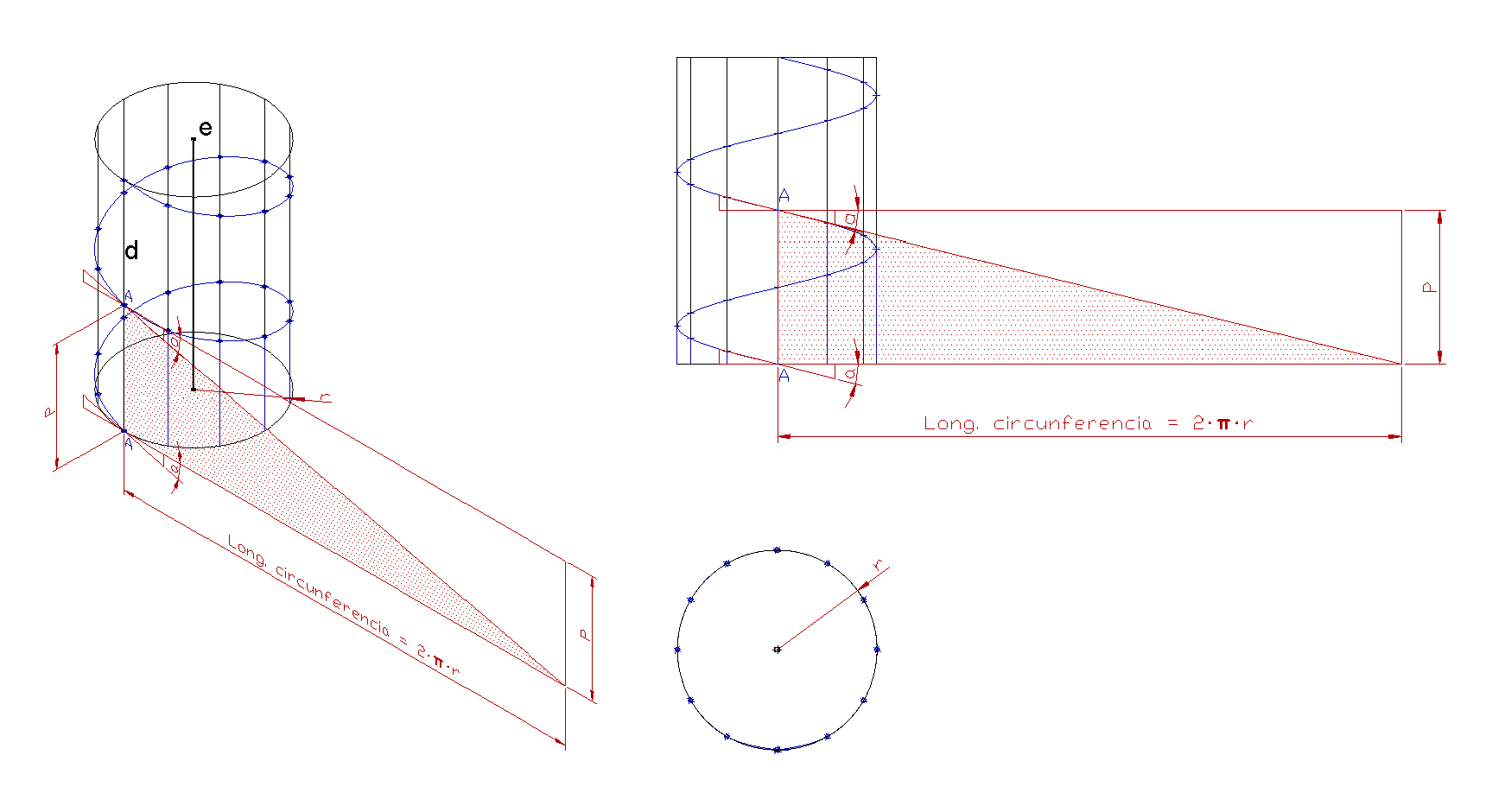
Es la curva engendrada por un punto A que se mueve uniformemente a lo largo de una recta directriz d, a la vez que esta gira con velocidad uniforme alrededor de un eje e y paralelamente a él a una distancia r.
Es la curva engendrada por un punto A que se mueve uniformemente a lo largo de una recta directriz d, a la vez que esta gira con velocidad uniforme alrededor de un eje e y paralelamente a él a una distancia r.
Elementos.
- El cilindro de revolución engendrado por la directriz d y de radio r, es el cilindro eje y radio de la hélice.
- En un giro de 360º de la recta directriz, el punto describe una curva llamada espira de altura P denominada paso de la hélice o paso de rosca.
|
Más artículos
Cad-Projects espera que los artículos sean de utilidad.
Si es así puedes imprimir una copia o recomendar a algún amigo usando los iconos de la barra superior. Visita nuestro FORO. Si tienes dudas o preguntas sobre algun tema allí podras resolverlas.





